4.「图」的广度优先搜索算法
既然我们之前已经提及了「深度优先搜索」算法了,那么作为它的兄弟算法「广度优先遍历」算法,我们就不得不提了。「广度优先搜索」算法不仅可以遍历「图」的所有顶点,也可以遍历两个顶点的所有路径。但是,「广度优先搜索」最高效的用途是:当在 权重相等且均为正数的「图」 中,它可以快速的找到两点之间的最短路径。
虽然「深度优先搜索」算法也可以针对权重相等均且为正数的「图」找出两点之间的最短路径,但它需要先找出两点之间的所有路径之后,才可以求出最短路径。但是对于「广度优先搜索」,在大多数情况下,它可以不用找出所有路径,就能取出两点之间的最短路径。除非,最短路径出现在最后一条遍历的路径上,这种情况下,「广度优先搜索」也是遍历出了所有路径后,才取出的最短路径。
如「图7. 无向图」所示,它的所有顶点分别为[A, C, D, B, E]。给定顶点 A 和 B, 它们之间有两条路径,一条路径为[A, C, D, B],另一条路径为[A, E, B]。其中,[A, E, B]是顶点 A 和 B 之间的最短路径。
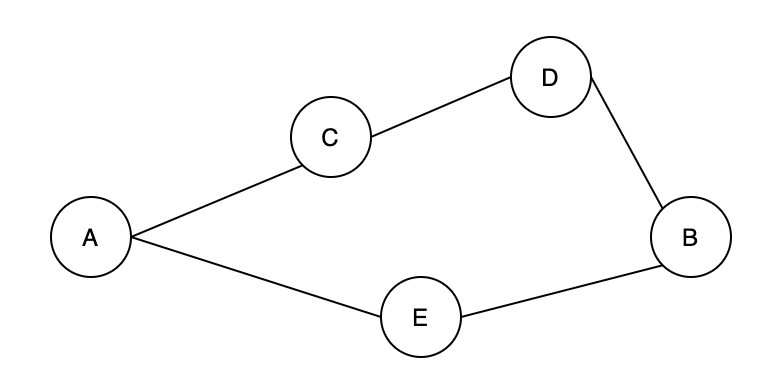
图7.无向图
「广度优先遍历」(又称「Breath First Search」,简称「BFS」)算法在「图」中主要用途:
- 遍历「图」中所有顶点;
- 针对 权重相等且均为正数的「图」,快速找出两点之间的最短路径。