2.3.按秩合并的「并查集」
小伙伴看到这里的时候,我们其实已经实现了 2 种「并查集」。但它们都有一个很大的缺点,这个缺点就是通过 union 函数连接顶点之后,可能所有顶点连成一条线形成「图 5. 一条线的图」,这就是我们 find 函数在最坏的情况下的样子。那么我们有办法解决吗?
当然,伟大的科学家已经给出了解决方案,就是按秩合并。这里的「秩」可以理解为「秩序」。之前我们在 union 的时候,我们是随机选择 x 和 y 中的一个根节点/父节点作为另一个顶点的根节点。但是在「按秩合并」中,我们是按照「某种秩序」选择一个父节点。
这里的「秩」指的是每个顶点所处的高度。我们每次 union 两个顶点的时候,选择根节点的时候不是随机的选择某个顶点的根节点,而是将「秩」大的那个根节点作为两个顶点的根节点,换句话说,我们将低的树合并到高的树之下,将高的树的根节点作为两个顶点的根节点。这样,我们就避免了所有的顶点连成一条线,这就是按秩合并优化的「并查集」。
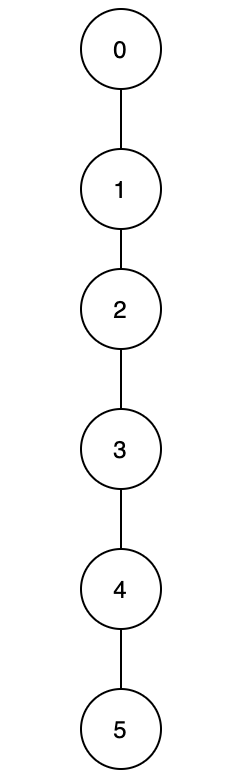 图5.一条线的图
图5.一条线的图
伪代码
// UnionFind.class
public class UnionFind {
int root[];
int rank[];
public UnionFind(int size) {
root = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
root[i] = i;
rank[i] = 1;
}
}
public int find(int x) {
while (x != root[x]) {
x = root[x];
}
return x;
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (rank[rootX] > rank[rootY]) {
root[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
root[rootX] = rootY;
} else {
root[rootY] = rootX;
rank[rootX] += 1;
}
}
};
public boolean connected(int x, int y) {
return find(x) == find(y);
}
}
// App.java
// 测试样例
public class App {
public static void main(String[] args) throws Exception {
UnionFind uf = new UnionFind(10);
// 1-2-5-6-7 3-8-9 4
uf.union(1, 2);
uf.union(2, 5);
uf.union(5, 6);
uf.union(6, 7);
uf.union(3, 8);
uf.union(8, 9);
System.out.println(uf.connected(1, 5)); // true
System.out.println(uf.connected(5, 7)); // true
System.out.println(uf.connected(4, 9)); // false
// 1-2-5-6-7 3-8-9-4
uf.union(9, 4);
System.out.println(uf.connected(4, 9)); // true
}
}
时间复杂度
| UnionFind 构造函数 | find 函数 | union 函数 | connected 函数 | |
|---|---|---|---|---|
| 时间复杂度 | O(N) | O(logN) | O(logN) | O(logN) |
注:N 为「图」中顶点的个数。