2.并查集
如果给你一些顶点,并且告诉你每个顶点的连接关系,你如何才能快速的找出两个顶点是否具有连通性呢?
如「图 5. 连通性问题」,该图给出了顶点与顶点之间的连接关系,
那么,我们如何让计算机快速定位 (0, 3) , (1, 5), (7, 8) 是否相连呢?此时我们就需要机智的「并查集」数据结构了。
很多地方也会称「并查集」为算法。
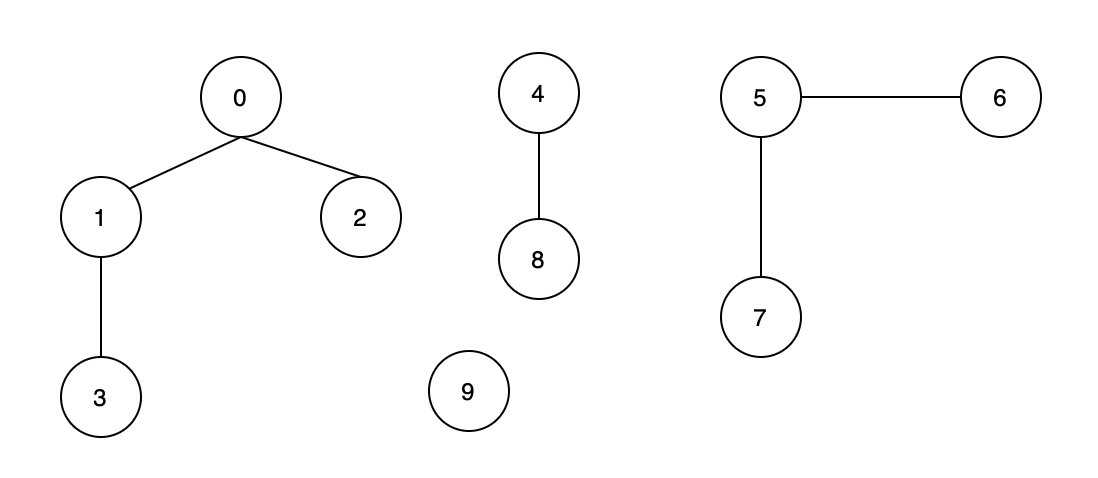 图5.连通性问题
图5.连通性问题
「并查集」的主要作用是用来解决网络中的连通性。这里的「网络」可以是计算机的网络, 也可以是人际关系的网络等等。例如,你可以通过「并查集」来判定两个人是否来自同一个祖先。
「并查集」常用术语
- 父节点:顶点的直接父亲节点。如「图5. 连通性问题」中,顶点 3 的父节点是 1;顶点 2 的父节点是 0;顶点 9 的父节点是自己本身 9。
- 根节点:没有父节点的节点,本身可以视为自己的父节点。如「图5. 连通性问题」中,顶点 3 和 2 的根节点都是 0;0 即是自己本身的父节点,也是自己的根节点;顶点 9 的根节点是自己本身 9。
「并查集」基本思想
//todo::
「并查集」编程思想
//todo::
「并查集」的两个重要函数
- find 函数:找到给定顶点的根结点。如「图5. 连通性问题」中,find 函数需要找到顶点 3 的根结点是 0 。
- union 函数:合并两个顶点,并将他们的根结点保持一致。如「图5. 连通性问题」中,如果我们需要将顶点 4 和 顶点 5 合并,那么顶点 4 和 顶点 5 至少需要保持根节点一致,也就是说 union 函数需要将顶点 4 和 顶点 5 的根结点修改为相同的根结点。
「并查集」的两个实现方式
- Quick Find 实现方式:它指的是实现「并查集」时,find 函数时间复杂度很低为 O(1)O(1),但对应的 union 函数就需要承担更多的责任,它的时间复杂度为 O(N)O(N)。
- Quick Union 实现方式:它指的是实现「并查集」时,相对于 Quick Find 的实现方式,我们通过降低 union 函数的职责来提高它的效率,但同时,我们也增加了 find 函数的职责。