1.「图」的基本知识
「图」大概是最接近生活的一种数据结构了,生活中各种关系图便是「图」最真实的写照。比如,我们每个人的朋友交际圈就是一个巨大的「图」。
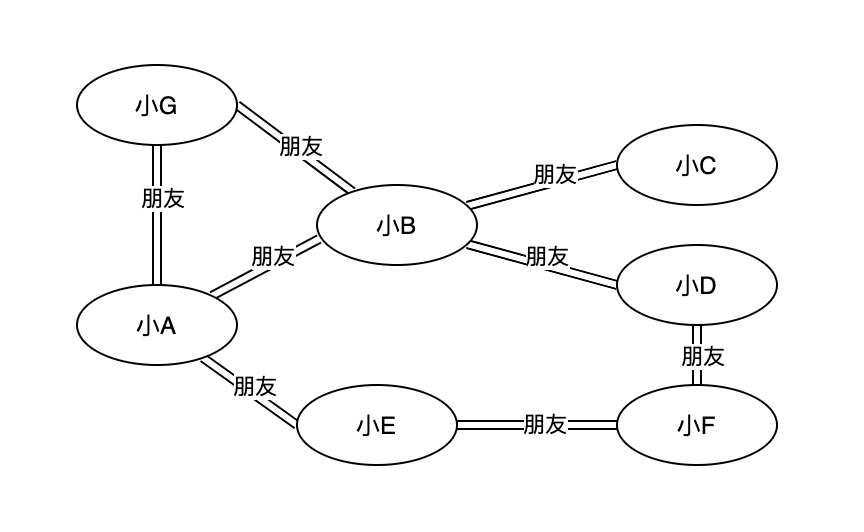 图1.小A的朋友交际图
图1.小A的朋友交际图
「图」的类型
「图」的类型有很多,我们将介绍三种类型的图:无向图、有向图、加权图。
无向图
「无向图」的图中任意两个顶点之间的边都是没有方向的。 「图1. 小A的朋友交际图」是一个无向图。
有向图
「有向图」的图中任意两个顶点之间的边都是有方向的。
「图 2. 有向图的示例图」是一个有向图。
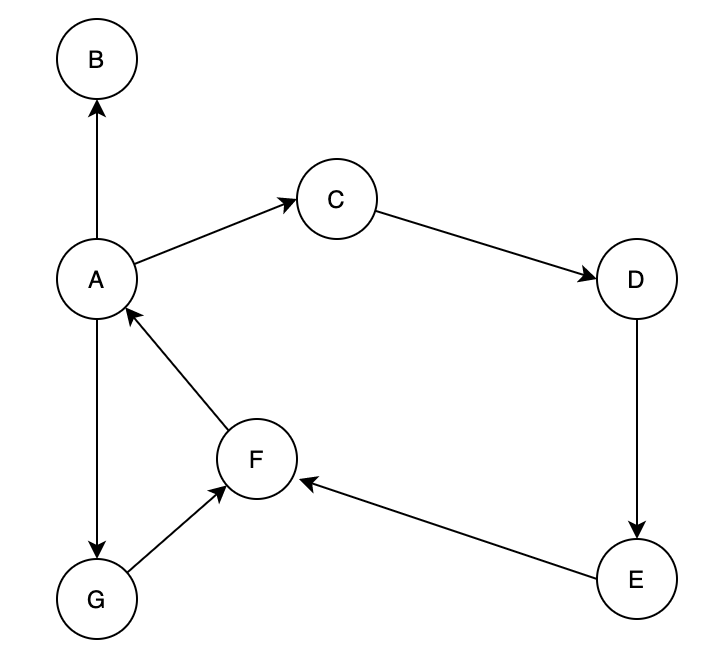 图2.有向图的示例图
图2.有向图的示例图
加权图
「加权图」的图中的每条边都带有一个相关的权重。这里的权重可以是任何一种度量,比如时间,距离,尺寸等。生活中最常见的「加权图」应该就是我们的地图了。在下方的「图 3. 加权图的示例图」中,每条边上都标有距离,它们可以视为每个边上的权重。
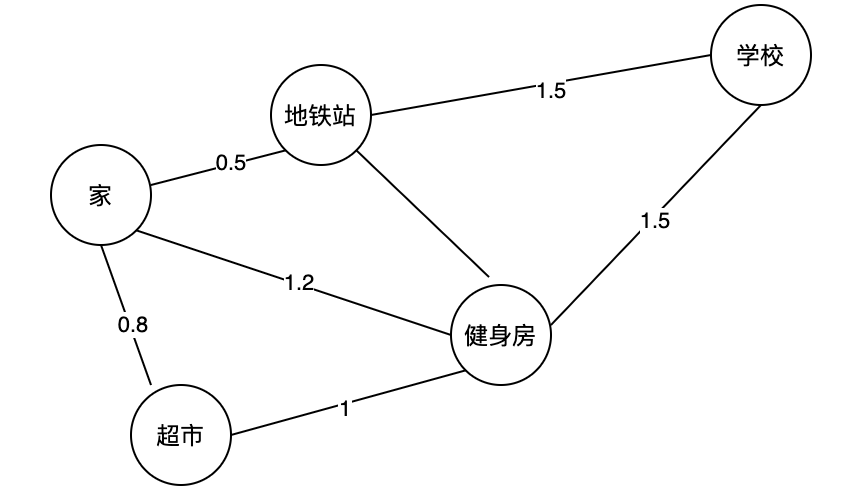 图3.加权图的示例图
图3.加权图的示例图
「图」的定义和相关术语
「图」是由顶点和边组成的一种非线形数据结构。在「图」中有很多相关术语来描述一个图。如果在后面的学习中遇到不认识的术语,请回到这里查看相关的定义。
- 顶点:在「图 1. 小A的朋友交际图」中,小 A 、小 B 、小 C 等均称为「图」的顶点。
- 边:顶点之间的连接线称为边。在「图 1. 小A的朋友交际图」中,小 A 和小 B 之间的连接线就是图中的一条边。
- 路径:从一个顶点到另一个顶点之间经过的所有顶点的集合。在「图 1. 小A的朋友交际图」中,从小 A 到小 C 的路径为[小A, 小B, 小C] 或者[小A, 小G, 小B, 小C]或者[小A, 小E, 小F, 小D, 小B, 小C]。 **注意:**两个顶点之间的路径可以是很多条。
- 路径长度:一条路径上经过的边的数量。在「图 1. 小A的朋友交际图」中,从小 A 到小 C 的路径长度为2或者3或者5。
- 环:起点和终点为同一个顶点的路径。在「图 1. 小A的朋友交际图」中,[小A, 小B, 小D, 小F, 小E]组成了一个环。同理,[小A, 小G, 小B]也组成了一个环。
- 负权环:在「加权图」中,如果一个环的所有边的权重加起来为负数,我们就称之为「负权环」。在「图4. 负权环」中,它的所有边的权重和为-3。
- 连通性:两个不同顶点之间存在至少一条路径,则称这两个顶点是连通的。在「图 1. 小A的朋友交际图」中,小 A 和小 C 是连通的,因为它们之间至少有一条路径。
- 顶点的度:「度」适用于无向图,指的是和该顶点相连接的所有边数称为顶点的度。在「图 1. 小A的朋友交际图」中,顶点小A的度为3,因为与它相连接的边有3条。
- 顶点的入度:「入度」适用于有向图,一个顶点的入度为dd,则表示有dd条与顶点相连的边指向该顶点。在「图 2. 有向图的示例图」中,A的入度为1,由F指向A的边。
- 顶点的出度:「出度」适用于有向图,它与「入度」相反。一个顶点的出度为dd,则表示有dd条与顶点相连的边以该顶点为起点。在「图 2. 有向图的示例图」中,A 的出度为3,分别为,A 指向 B 的边,A 指向 C 的边,和 A 指向 G 的边。
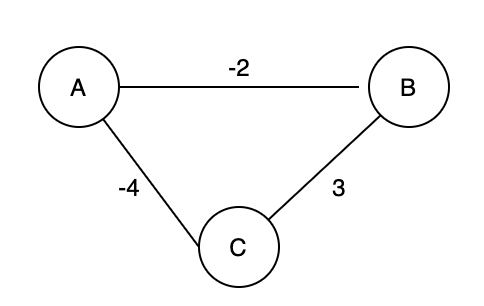 图4.负权环
图4.负权环